Borg MOEA 
The Borg Multiobjective Evolutionary Algorithm (Borg MOEA) features auto-adaptive multi-operator search, dynamic population sizing, and epsilon-dominance archiving to solve many-objective optimization problems. See our publications for details on its design as well as studies demonstrating the effectiveness and efficiency of the Borg MOEA on a number of real-world applications. The C/C++ source code is freely available for academic and non-commercial use. Visit http://www.borgmoea.orgfor more information and to request access to the source code.
Who uses Borg? The network below shows collaborators who have worked together and cite Borg in shared publications.
Interactive Parallel Axis Plots
- Interactive parallel axis plots Built with Parcoords D3.js library. Upload a CSV data file to explore tradeoffs between conflicting objectives.
- Interactive parallel axis plots with groups Built with Parcoords D3.js library. Upload a CSV data file to explore tradeoffs between conflicting objectives of grouped data.
MOEA Benchmark Problems
Reed, P. et al. 2013 (Link to Paper)
Benchmark optimization problems published in “Evolutionary multiobjective optimization in water resources: The past, present, and future”, an invited submission to the 35th Anniversary Issue of Advances in Water Resources. The problems are intended for use with MOEAFramework but may be modified for other algorithms or libraries.
MOEA Framework
MOEA Framework is a free, open-source Java framework for experimenting with several popular MOEAs including GDE3, MOEA/D, NSGA-II, ε-MOEA, ε-NSGA-II and random search. These MOEAs can be run on over 80 test problems, including problems from the ZDT, DTLZ and WFG test problem suites, as well as all constrained and unconstrained problems from the IEEE CEC 2009 special competition. The framework and source code can be downloaded from http://www.moeaframework.org. New users connecting their own optimization problems to MOEAFramework are encouraged to read through the MOEAFramework Setup Guide.
Interested users may also explore the in-browser MOEA Diagnostic Tool (requires Java).
OpenMORDM 
Hadka, D., Keller, K., & Reed,P.(Link to Paper)
Robust Decision Making (RDM) is an analytic framework developed by Robert Lempert and his collaborators at RAND Corporation that helps identify potential robust strategies for a particular problem, characterize the vulnerabilities of such strategies, and evaluate trade-offs among them [Lempert et al. (2006)]. Multiobjective Robust Decision Making (MORDM) is an extension of RDM to explicitly include the use of multiobjective optimization to discover robust strategies and explore the tradeoffs among multiple competing performance objectives [Kasprzyk et al. (2013)].
- Interactive R Tutorial by D. Hadka 2015
Open-Source Models
- Hymod and HBV rainfall-runoff models in C/C++. Written for use with MOPEX hydrologic data, but can be modified for use with other forcing and response data. Based on work from this paper but later modified for generality.
Project Platypus
A collection of libraries for optimization, data analysis, and decision making that includes that following:
- PRIM, a Python library for the Patient Rule Induction Method, an algorithm for classifying binary data into hyper-dimensional boxes
- Rhodium, a Python library for exploratory modeling and Robust Decision Making (RDM)
- J3, a free desktop application for producing and sharing high-dimensional, interactive scientific visualizations
- Platypus, a free and open source python library for multi-objective optimization
- J3Py, a free desktop application for producing and sharing high-dimensional, interactive scientific visualizations
- Executioner, a cross-language automation tool for running models
PySedSim
Wild et al. 2020 (Link to paper)
PySedSim is an open-source, object-oriented, Python-based daily time step river basin simulation model for flow, sediment, and hydropower production in networks of reservoirs and river channels. It is intended to predict in relative terms the spatial and temporal accumulation and depletion of sediment in river reaches and in reservoirs under different reservoir operating and sediment management policies. The model can be run in both stochastic (Monte Carlo) and deterministic modes. It also offers integrated support for coupling with an external evolutionary optimization algorithm to identify tradeoffs among operating policies designed to perform well across a suite of user-defined objectives. The software is available at: https://github.com/FeralFlows/PySedSim
Sensitivity Analysis Library (SALib)
- SALib, a Python library containing Sobol, Morris, and FAST sensitivity analysis methods. Requires Numpy. Designed for decoupled analysis, where sampling, model evaluation, and analysis steps are all performed separately.
UC eBook: Addressing Uncertainty in Multisector Dynamics Research

We are pleased to announce that we have published our free eBook on Addressing Uncertainty in Multisector Dynamics Research, a primer on uncertainty characterization methods for research on sustainability, climate, and human-natural systems. You can find this eBook here
This eBook is the product of years of collaboration across several teams that brings in perspectives from natural sciences, decision making under (deep) uncertainty, software engineering, statistics, and risk analysis. The breakdown of the book is as follows:
Chapter 1 uses the IM3 project as a living lab to encapsulate the challenges that emerge in bridging disciplines to make consequential model-based insights while acknowledging the tremendous array of uncertainties that shape them.
Chapter 2 helps the reader to better understand the importance of using diagnostic modeling and the diverse disciplinary perspectives that exist on how best to pursue consequential model-based insights.
Chapter 3 is a technical tools-focused primer for readers on the key elements of uncertainty characterization that includes ensemble-based design of experiments, quantitative methods for computing global sensitivities, and a summary of existing software packages.
Chapter 4 narrates for readers how and why the tools from the previous chapter can be applied in a range of tasks from diagnosing model performance to formal exploratory modeling methods for making consequential model-based discoveries.
The supplemental appendices provide a glossary, a brief summary of uncertainty quantification tools, and a suite of Jupyter notebook tutorials that provide hands-on training tied to the contents of Chapters 3 and 4.
A central theme of this eBook is that it is a living document that will be actively maintained through its GitHub repository. If you work on exploratory modeling, sustainability, management of human-natural systems, complex systems or adjacent areas we’d love your feedback on how the document could be improved! You can open an issue here.
WaterPaths
Trindade et al. 2020 (Link to paper)
WaterPaths is a generalizable, cloud-compatible, open-source exploratory modeling system designed to inform long-term regional investments in water infrastructure while simultaneously aiding regions to improve their short-term weekly management decisions, often made in response to droughts. WaterPaths has the capability to identify coordinated planning and management for groups of water utilities sharing water resources. WaterPaths’ exploits dynamic and adaptive risk-of-failure (ROF) rules to trigger management and planning actions in temporally consistent pathways. The C++ source code and instructions for use can be found at: https://github.com/bernardoct/WaterPaths
Pywr-DRB
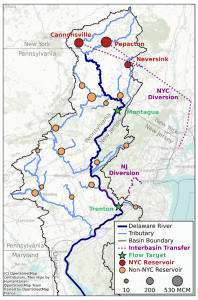
Pywr-DRB is an open-source Python model for exploring the role of reservoir operations, transbasin diversions, minimum flow targets, and other regulatory rules on water availability and drought risk in the DRB. Pywr-DRB is designed to flexibly draw on streamflow estimates from a variety of emerging data resources, such as the National Water Model, the National Hydrologic Model, and hybrid datasets blending modeled and observed data. Pywr-DRB bridges state-of-the-art advances in large-scale hydrologic modeling with an open-source representation of the significant role played by the basin’s evolving water infrastructure and management institutions. Pywr-DRB version 1.0 is available on GitHub: https://github.com/Pywr-DRB/Pywr-DRB/
Some training materials are available on our lab manual site here.
For more details, see the following paper:
Hamilton, A.L., Amestoy, T.J., & P.M. Reed. (2024). Pywr-DRB: An open-source Python model for water availability and drought risk assessment in the Delaware River Basin. *(In Review)*. Preprint accessible here: https://ssrn.com/abstract=4765247.